Breakthrough: a first-in-class virtual simulator for dose optimization ... - Nature.com
Abstract
The renin–angiotensin–aldosterone-systems (RAAS) play a central role in the pathophysiology of congestive heart failure (CHF), justifying the use of angiotensin converting enzyme inhibitors (ACEi) in dogs and humans with cardiac diseases. Seminal studies in canine CHF had suggested that the pharmacological action of benazepril was relatively independent of doses greater than 0.25 mg/kg P.O, thereby providing a rationale for the European labeled dose of benazepril in dogs with CHF. However, most of these earlier studies relied on measures of ACE activity, a sub-optimal endpoint to characterize the effect of ACEi on the RAAS. The objectives of this study were (i) to expand on previous mathematical modeling efforts of the dose-exposure–response relationship of benazepril on biomarkers of the RAAS which are relevant to CHF pathophysiology and disease prognosis; and (ii) to develop a software implementation capable of simulating clinical trials in benazepril in dogs bedside dose optimization. Our results suggest that 0.5 mg/kg PO q12h of benazepril produces the most robust reduction in angiotensin II and upregulation of RAAS alternative pathway biomarkers. This model will eventually be expanded to include relevant clinical endpoints, which will be evaluated in an upcoming prospective trial in canine patients with CHF.
Introduction
Although the exact pathophysiology of the heart diseases underlying congestive heart failure (CHF) differ between man and his best friend, overactivation of the renin–angiotensin–aldosterone system (RAAS) plays a key role in the pathogenesis and development of CHF in both humans and dogs. To reduce RAAS activation, there is a substantial history of using ACEis, such as benazepril, to treat CHF in both species1,2,3. This makes the use of benazepril to treat CHF in canines and humans an excellent case study for applying the One Health Initiative paradigm. This paradigm recognizes that accumulating data on the effect of therapeutics on CHF in canines has the potential to benefit therapeutic management of CHF in humans and vice versa4.
The RAAS is a neurohormonal compensatory system which primarily manages blood volume and pressure by modulating electrolyte transport and vascular tone. The contemporary model of RAAS activation has two main components. The classical RAAS pathway refers to the peptide cascade from angiotensinogen to angiotensin I (AngI), and then from AngI to angiotensin II (AngII). These enzymatic reactions are catalyzed by renin and ACE, respectively, and ultimately lead to increased aldosterone (ALD) production (see Fig. 1;4). Short-term physiologic consequences of classical RAAS activation include vasoconstriction, renal sodium and water retention, and increased blood pressure. Long-term physiological consequences include fluid overload, increased cardiac afterload, and myocardial and vascular fibrosis5,6,7,8,9. Essentially, chronic long-term classical RAAS activation both contributes to, and is stimulated by, the development of CHF10,11, while classical RAAS pathway downregulation has been associated with improved long-term prognosis in CHF9,12,13,14,15. The alternative RAAS pathway acts as a counterregulatory mechanism against classical pathway activation. Activation of the alternative RAAS pathway is characterized by catalysis of AngII to angiotensin (1–7) (i.e. Ang(1–7)) by the enzyme ACE2. In turn, Ang(1–7) activates Mas receptors leading to vasodilatation, diuresis, and natriuresis16. Via this physiological effect, chronic alternative RAAS activation in CHF has been associated with reduced risk of heart failure in patients with reduced and preserved ejection fraction. An ideal therapeutic drug candidate for CHF would therefore modulate both pathways at once, downregulating the activity of the classical RAAS while preserving or upregulating the alternative RAAS pathway13. However, little is known about the effect of benazepril on the alternative RAAS in either humans or dogs.
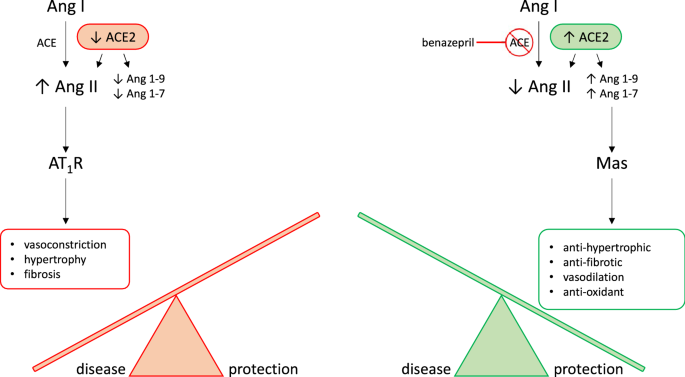
Biological arms of the RAAS. RAAS activation is thought of as having two main pathways which act as counterregulatory mechanisms for one another. The classical RAAS pathway (in red orange) refers to the peptide cascade from angiotensin I (Ang I) to angiotensin II (Ang II) via ACE. This stimulates aldosterone production which then activates AT1 receptors (AT1R). Physiologic consequences of classical RAAS activation, including vasoconstriction, hypertrophy, and fibrosis, typical worsen congestive heart failure (CHF). Benazepril inhibits ACE, therefore activating the alternative RAAS pathway (in green). Activation of the alternative RAAS pathway is characterized by catalysis of Ang II to Ang1-7 by the enzyme ACE2. In turn, Ang1-7 activates Mas receptors leading to vasodilatation, diuresis, and natriuresis. These effects are protective against CHF. Our goal is to use mathematical modeling to determine a dosage which both reduces classical RAAS pathway activation and stimulates alternative RAAS pathway activation. This hypothetical dosage would maximize CHF-protective effects of benazepril.
Benazepril hydrochloride is a non-sulfhydryl ACEi commonly used for the management of CHF in both humans and dogs. Like other ACEi, benazepril is a prodrug that is rapidly converted through hydrolysis to its active benazeprilat by esterases, mainly in the liver17. Although frequently prescribed, the recommended dosage range of benazepril is quite broad and there is no clear consensus on the ideal dose to be used in patients with CHF. In humans, benazepril is typically prescribed for hypertension at an initial dose of 2.5–10 mg per day and up titrated to 20 or 40 mg per day, administered either once or twice daily (q24h or q12h) which is roughly equivalent to 0.5 mg/kg q12h for a 60 kg adult18. In dogs, the labeled dose of benazepril in the EU is 0.25–1.0 mg/kg PO q24h, whereas ACVIM veterinary consensus statements recommend a dose of 0.5 mg/kg PO q12h19. Pharmacokinetic (PK) and pharmacodynamic (PD) studies comparing various doses of benazepril in healthy dogs have not provided consistent recommendations to date. The study that was used for registration of benazepril in the EU showed that a single PO dose of benazepril effectively suppressed ACE activity for up to 24 h, and that ACE inhibition in plasma was independent of dosage ≥ 0.25 mg/kg2. However, subsequent reanalysis of these data using mathematical modeling suggested that q12h dosing (as opposed to q24h dosing) would achieve greater inhibition of ACE with the same q24h total dose20. Furthermore, a different study of single dose enalapril and benazepril at a dosage of 0.5 mg/kg indicated a much shorter duration of effect, with ACE suppression lasting < 12 h21, and a recent retrospective study in dogs with valvular heart disease suggested improved outcomes with q12h dosage22.
There are several reasons why developing consistent recommendations for dosing of ACEi has proven challenging in veterinary medicine. Historically, ACE activity was used as a surrogate for RAAS activity. Recently, however, ACE activity has been shown to be an inefficient measure of RAAS activation. Numerous studies in humans and dogs have shown a lack of correlation between circulating ACE activity and Ang II concentrations4,23. A second challenge in developing scheduling recommendations is the significant chronobiological modulation of the RAAS. Previous experimental models of RAAS activation failed to consider the chronobiology of the RAAS, while contemporary research has shown that biomarkers of the renin pathway are subject to circadian variations in dogs4,23,24. Finally, existing PKPD studies on the effect of various ACEi have not consistently sampled biomarkers of alternative RAAS activation in addition to biomarkers of classical RAAS activation.
Overall, although the effects of ACEi, such as benazepril, on ACE activity have been fairly well characterized, and the benefit of ACE inhibition in CHF has been definitively established in several clinical trials in both humans and dogs (0.25 to 1.0 mg/kg q12h-q24h), little is known about the effect of benazepril on the alternative RAAS pathway in either species. Understanding the dose-dependent effects of benazepril on biomarkers of both the classical and alternative RAAS pathways in dogs would allow exploration of benazepril dosages that produce a downregulation of the classical RAAS while preserving, or upregulating, the alternative RAAS. This would translate into an optimization of the clinical benefit. Accumulating data that inform such a nuanced approach to dose optimization in dogs would provide valuable translational information for similar dose optimization of ACEi in humans. To model and predict the dose-dependent effects of benazepril on the classical and alternative arm of the RAAS, we aimed to build a nonlinear mixed-effects (NLME) model of benazepril PKPD. NLME modeling of benazepril PKPD had already previously been shown to be an efficient method for describing the effect of benazepril on the classical RAAS in canines and is a well-accepted framework for building PKPD models11.
To produce data for this modeling and simulation effort, nine healthy beagles were intensively sampled while administered benazepril at various dosages and frequencies. After producing the data, our objective was to use a quantitative-systems pharmacology (QSP) model to characterize the PKPD relationship of benazepril(at) on biomarkers of the RAAS which are relevant to CHF pathophysiology and associated with morbidity/mortality {angiotensins I, II, III, IV, (1–7)}. QSP modeling is a subgroup of PKPD models which seeks to describe the behavior of a pharmaceutical in terms of the biology of its mechanism of action. After developing and calibrating the model, we further developed a software implementation of the benazeprilat-RAAS QSP model, which is capable of rapidly simulating the effect of benazepril HCL at various doses in a larger population of virtual dogs. By developing an easy-to-use simulation interface for our model, the objective of this work was to make a first prediction of the optimal dose/time of benazepril administration in dogs in support of future investigations in patients with CHF.
Results
Animal safety
All study dogs received all oral doses of benazepril as intended. Dogs were monitored for adverse effects associated with benazepril labeling as well those associated with general animal welfare e.g., vomiting, diarrhea, inappetence, weakness/hypotension, fatigue, incoordination, hypercreatininemia. No adverse effects were observed in the animals during the course of the study, and serial complete blood counts and chemistry panels performed showed no evidence of hematologic or biochemical abnormalities from benazepril dosing.
Data mining
Data were collated and standardized for mathematical modeling as instructed in the Monolix documentation25. Except for standardization of units as molar amounts and concentrations, raw data were left untransformed. Doses were transformed using the molecular weight of benazepril HCl, while concentrations were transformed using the molecular weight of the active metabolite–benazeprilat. Data were reviewed for bulk trends and data quality both before, during, and after mathematical modeling.
Data below the lower limit of quantification (LLOQ) were modeled by adding to the likelihood function a term describing the probability that the true observation lies between zero and the LLOQ, which is equivalent to the M3 method implemented in the NONMEM (Non-linear Mixed Effects Modeling) software.
The log10 time-course of benazeprilat as well as the relevant RAAS biomarkers are reproduced in Fig. 2. Of note, there was some background experimental noise in pharmacodynamics of some biomarkers that ultimately reduced model prediction quality. The noise was most prominent in the biomarker Angiotensin III (2–8) (i.e. AngIII), where the order of the limit of quantification (2.5 pmol/L) was approximately half of the measurement at the 3rd quartile (5.1 pmol/L). Suspected outliers were flagged and tested as model covariates for statistical significance. However, none of the flagged data points were determined to be significant enough outliers to exclude from model building.
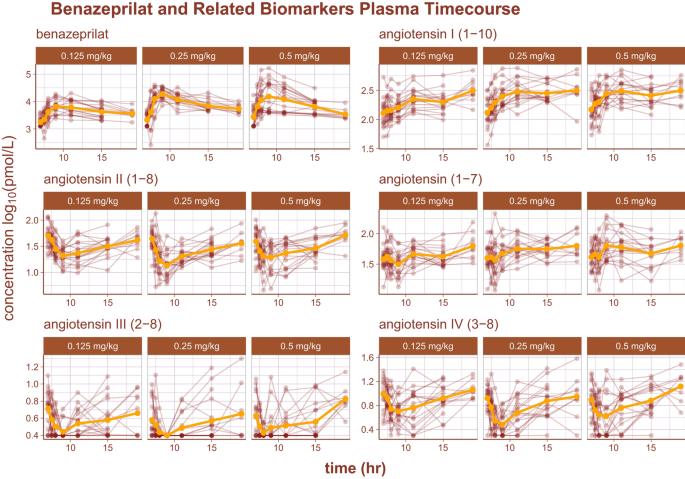
RAAS biomarkers pharmacodynamics. An overview of the plasma time-course of several RAAS biomarkers as well as benazepril's active metabolite, benazeprilat. Each subject's time-course is indicated with a red line and points. The golden curve is the mean time-course value.
Following is a summary of the model building process. The base empirical version of the full model was largely an adaption of the benazeprilat PKPD model reported in Mochel et al.23. In all, over 100 different structural modifications were tested, starting from the empirical base model, to produce our final QSP model. To simplify results reporting, the most important modifications tested are summarized in the following two sections. Despite the division of sections into PK and PD, after building a base model to work from, all model fits were performed on the full PKPD dataset.
PK model building
The PK portion of the base model was a conventional 2-compartment mammillary model with saturable exchange between the central and peripheral compartments. Building on this initial model, several modifications of the PK structure were evaluated. First, several standard compartment variations were tested i.e., using 1-, 2-, or 3-compartment disposition functions. Overall, a 2-compartment PK model outperformed the other candidate models based on the precision of individual parameters and overall quality of fit. Second, non-specific (low affinity, high capacity) binding of benazeprilat to plasma proteins was represented by a 3rd compartment within the central compartment, i.e., representing the free circulation of benazeprilat. The volume of the non-specific binding compartment (Vns) is a representation of the relative binding capacity of benazeprilat which is distributed in plasma but is not freely circulating or interacting with ACE. Therefore, the total amount of measurable benazeprilat in plasma is a combination of the amount non-specifically bound to plasma proteins (Ins) (low affinity, high capacity), the amount specifically bound to ACE (high affinity, low capacity) and the amount of benazeprilat in free circulation (Ifree)4,20. The variable I was chosen to represent benazeprilat as it inhibits ACE activity.
Zero-, first-, mixed-, and sequential absorption structures were tested to model drug absorption from the depot compartment (i.e., intestinal lumen). A model largely equivalent to sequential absorption, but made to be continuous, was found to outperform other competitive models. This model substructure uses a series of 1-order absorptions but can be seen as a continuous analog to a sequential 0-/1-order absorption.
In this model, the first depot compartment for benazepril after oral administration was called 1abs. First-order absorption either occurred immediately at rate ka1 to the compartment of freely circulating benazeprilat (fr), or absorption was delayed by an absorption rate ka through an intercompartment that was pre-circulatory (pr). As is typical, quantity of benazeprilat passed between compartments is called Im, n, for inhibitor, where indexes m and n represent origin and destination compartments, respectively. Fbio represents the total bioavailability (Eq. 1). Doses are administered in benazepril hcl, but are measured as the metabolite–benazeprilat. To reduce complexity in modeling, but preserve absorption and benazepril to benazeprilat conversion variance, all bioavailable benazepril is treated as benazeprilat in the model. Fbio, or total bioavailability, is estimated in the model purely to preserve this variance and to reduce numerical instability in estimation. However, without IV data, the final estimated Fbio does not have a firm pharmacological interpretation.
In summary, the final mammillary model without ACE binding kinetics (Eq. 2) was a 2-compartment PK model with nonspecific protein binding represented by a 3rd compartment (Ins), and a continuous analog to sequential 0-/1-order absorption from some depot compartment.
Rate of exchange between compartments were governed by rates kf, g where f and g (f ≠ g) were each one of either free circulation (fr), tissue (ts), or non-specifically bound in circulation (ns). Residual error was best modeled using a normal-proportional error function (Eq. 6). The only exception were rates of elimination which were written as kCl, d where clearance represented that the parameter was derived from clearance and d was the compartment of origin.
PKPD model building
Benazeprilat primary mechanism of action is inhibiting ACE to prevent the catalysis of AngI into AngII. To account for this mechanism, a logistic saturation model was first implemented. However, the superior model for predicting benazeprilat ACE inhibition was found to be the differential Michaelis–Menten model of catalysis inhibition with ACE being the enzyme (E), benazeprilat the inhibitor (I), AngI being the substrate (S) and AngII being the product (P) (Eq. 3). The distribution of ACE across tissue (ts) and free circulation (fr) was also considered. The nomenclature used throughout Eq. (3) is consistent with previous descriptions of the Michaelis–Menten model26.
Two-compartment mammillary models governed the kinetics of biomarkers AngI, AngII, and Ang(1–7). The amount in these compartments were respectively represented by S (substrate), P (product), and Ang(1–7). The two compartments for these angiotensins were called free circulation (fr) and tissue (ts). Conversion steps in the classical and alternative RAAS pathways were modeled through a series of catalytic steps, as previously described27.
At last, the function fCT(t) governs the effect of chronobiology on the production rate of the substrate (rs). fct(t) is a scaled cosine function where the wavelength (or period) is matched to 24 h, the relative maximum amplitude is the scalar PRA (peak renin amplitude), and the scale of that amplitude is governed by δ24hr. Chronobiology is herein only modeled relative to AngI production (Eq. 4).
The catalyses of AngII to AngIII, and AngIII to AngIV were modeled via a series of catalytic conversion models (Eq. 5). Cleavages of AngII to AngIII, and AngIII to IV, are primarily performed by renally-bound aminopeptidases A and N, respectively28,29,30. Vfree was subdivided into two circulatory system volumes of distribution; a small renal volume (Vrn) and a larger plasma volume (Vpl). All catabolism of AngII to AngIII, and AngIII to AngIV were linked to the renal volume as this is where aminopeptidases A and N are physiologically located.
All analytes residuals were best described by proportional error models (Eq. 6), with the concentration of a given biomarker scaled by ε. ε is a normal distribution distributed with standard deviation b, i.e. ε ~ N(0, b).
ANOVA tests on covariates indicated that model performance would not be significantly improved by the inclusion of any covariate effects. The full model written in Mlxtran is available in the supplemental files, and a model diagram detailing the full structure is reproduced in Fig. 3. In S1 Table, the reader can find a detailed description of all mathematical symbols defined in the "Results" section.
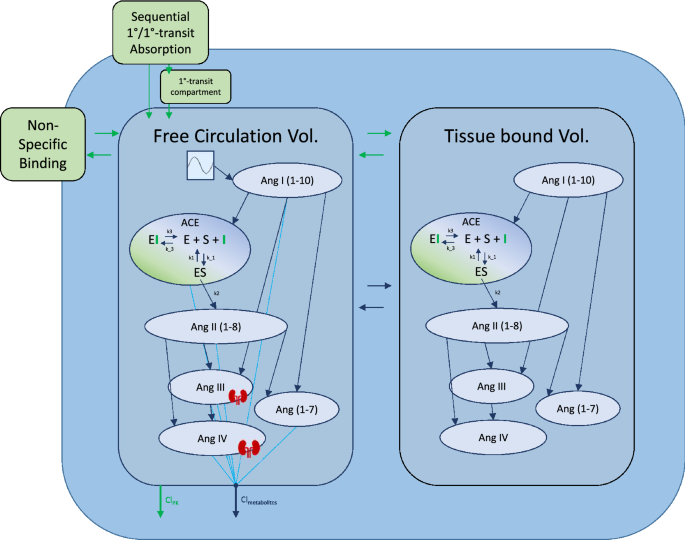
Detailed model diagram. Detailed diagram of the final model structure. Benazeprilat pharmacokinetics were modeled using a 2-compartment model with a mix of 1-order and 1-order delayed by 1-order transfer absorption from the depot compartment. Both volumes of distribution, free and tissue, were modeled with a fixed amount of ACE with which Benazeprilat could act on. Non-specific binding affected the free circulation compartment. A series of direct response models were used to describe the transformation of angiotensin I into its various metabolites. The free volume of distribution was subdivided into plasma and kidney volumes for Ang III and Ang IV. A Michaelis–Menten kinetic model of inhibitor, substrate, and enzyme interaction was used to describe the competitive inhibition of ACE by benazeprilat. k3 and k-3 were the parameters governing ACE-benazeprilat (enzyme-inhibitor) association and dissociation, while k1 and k-1 determined the rate of ACE-angiotensin (enzyme–substrate) association and dissociation. k2 controlled the production rate of angiotensin II from angiotensin I via ACE. An independent clearance for each metabolite as well as benazeprilat controlled the rate of removal of various molecules from the plasma.
Model fit evaluation
Inspection of the SAEM search and a sensitivity analysis on initial parameter values revealed a stable and precise search for all parameter estimates. The final selected model had high precision in parameter estimates as evaluated via RSE (majority of estimates < 35%). A summary of model parameter estimates, including typical value, RSE (%) and inter-individual variability (IIV) can be found in Table 1.
Inspection of goodness-of-fit summary plots (Figs. 4, 5, 6) indicate that benazeprilat predictions from the model are largely in line with experimental measurements. Importantly, the final PKPD model, which enabled the simultaneous fit of all angiotensins, was found to characterize the time-varying changes of the both the classical and alternative arm of the RAAS satisfactorily, as shown by the standard goodness-of-fit diagnostics of observations vs predictions (Fig. 4), the individual predictions (Fig. 5), and the simulation-based validation diagnostics (i.e., NPDEs, Fig. 6).
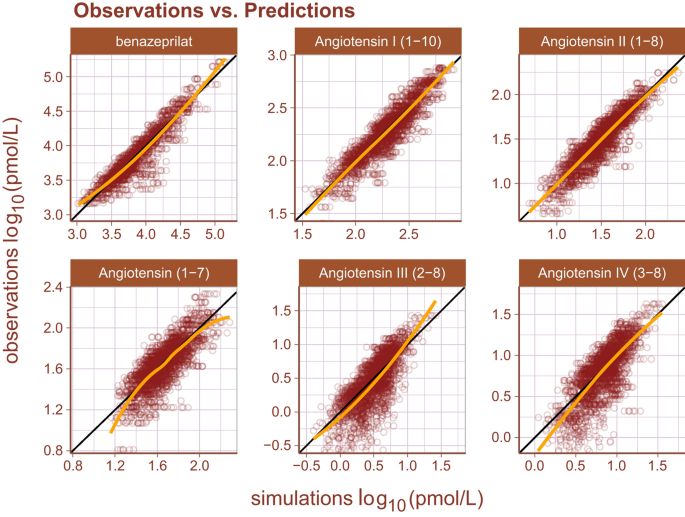
Observations vs predictions. The observations plotted against the predictions for all metabolites and drug concentration data. This gives a complete picture of model performance. The golden line is the LOESS curve showing the correlation between observations and predictions. The black line plotted diagonally represents an ideal model performance with no misspecification. The general agreement between LOESS and idealized curve indicates that there is little misspecification in model structure.
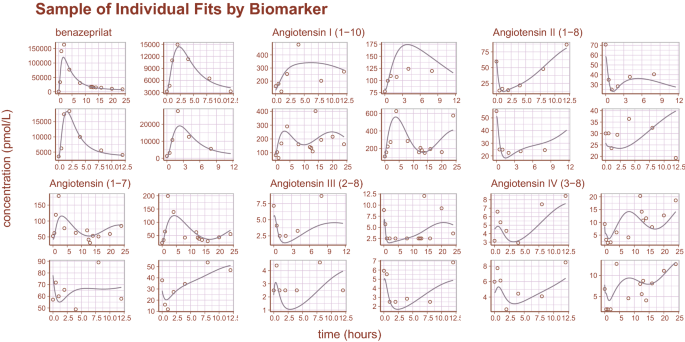
Sample of individual predictions. A sample of individual observations vs predictions randomly sampled from the concentration and metabolite data. The general agreement between plasma concentration time-course and individual predictions indicates that the model reproduces the observations with high accuracy.
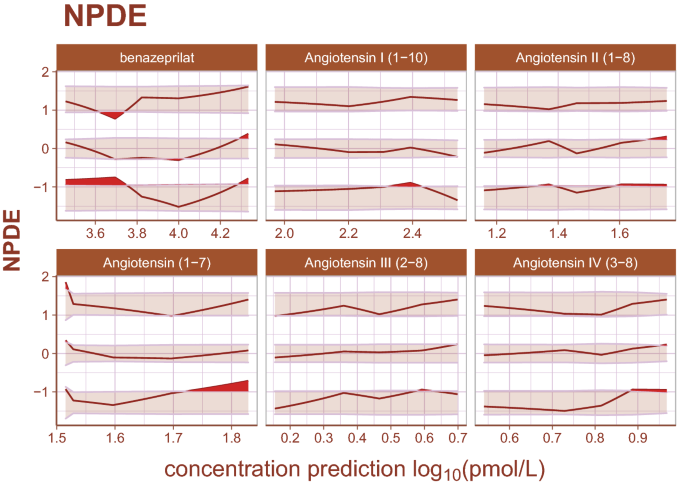
Normalized prediction distribution errors. Normalized prediction distribution errors (NPDEs) are an analog to residuals used for diagnosing both model structural misspecifications as well as the performance of the residual error model. The distribution of a well-specified model is normal, ideally. Bands represent the 90% prediction band for the 95th, 50th, and 5th percentiles, respectively. Curves are the observed percentiles for the 95th, 50th, and 5th percentiles, respectively. Data are binned at regular intervals to derive these average trends. For each binning range, if the structural model fits the data well, observed percentiles will be symmetrically distributed across a 50th percentile curve which falls within the 50th percentile band. If the error model is well specified, observed percentiles will fall within prediction bands. Any misspecification is ideally random. The model appears to underpredict angiotensin (1–7) for small measured values slightly, but otherwise there is high agreement between model and data.
Simulation engine
There are three primary views in this application (Fig. 7). In all views, the time of first dose of benazepril is specified in a 24-h clock format. On the left-hand side of the application is a menu for specifying dosing, parameters of the simulation, and modalities for calculating the area under the effect curve (AUEC) that quantifies the effect of the active benazeprilat on the RAAS at various doses vs. placebo control. Note that the application menu can be hidden to increase the size of the plotting area.
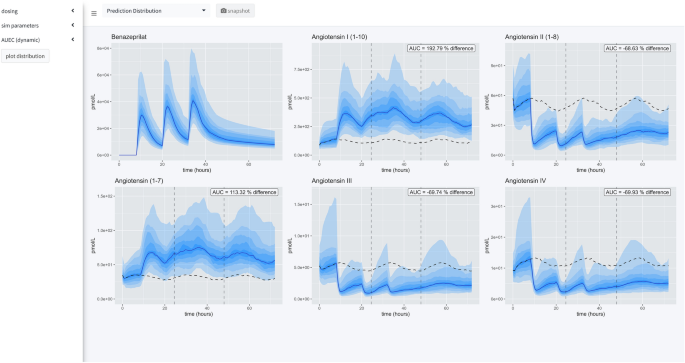
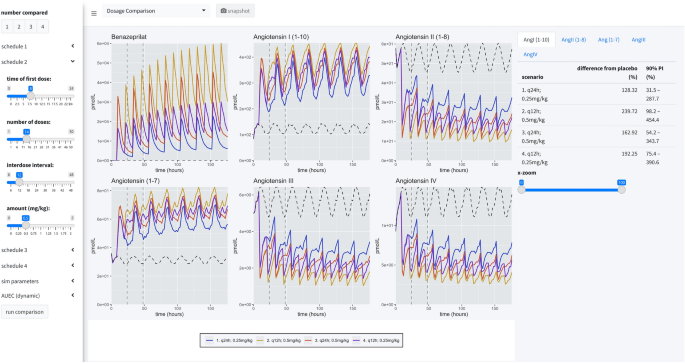
Application views. Our application provides a user-friendly way to apply our model of RAAS response to various administration schedules of benazepril. A collapsible left-hand widget allows the user to specify the simulation. The application has 3 separate panels. In the first panel, a single dosage scheme can be applied to a large simulated population of animals. Then the prediction distribution of simulated patient responses is plotted for study. In the second panel, the user can make a comparison between several proposed administration schedules. The plots produced in this panel depict the median time-course of the various metabolites in response to the proposed schedules. The user also has access to an x-axis zoom and AUC comparison summaries on the right-hand side. The final panel is simply documentation of the simulation engine code and tips for usage.
Application menu
The left-hand menu is split into three tabs which allow the user to define parameters of the simulation. The dosing tab permits the user to define the dosing schedule in terms of time of first dose, number of doses, size of dosage, and interdose interval. The simulation parameters tab gives the user access to the timescale of the simulation, the fineness of the grid used for simulation, and the sample size used to calculate the median and prediction intervals of the simulated PKPD. Finally, the AUEC tab provides a means to compare pharmacodynamic effects between competing dosing scenarios by defining a time period for which to calculate AUEC estimates.
Prediction distribution view
The first tab gives the user tools for analyzing the distribution of responses after a single schedule of benazepril. The distribution is specified in terms of median effect (blue line), median effect of placebo using same simulated individuals (dashed black line), and 90% prediction interval (blue bands) in steps of 10% i.e., 5% to 95%, 15% to 85%, etc. The AUEC of treatment vs. placebo can be compared for the timespan between the dashed vertical lines. The percent difference between those two AUECs is documented in the hovering label.
Dosage comparison view
The second panel allows the user to compare up to four competitive dosing schedules to placebo. In this panel, the user can see the median response (key at bottom) and the placebo effect (dashed black line), but not the distribution of responses. On the right-hand side of the page, the user can compare the percent difference from placebo in the RAAS components modeled in this study by paging through the various data tables. These comparisons are percentages relative to placebo.
Documentation view
The last view is simply documentation on the model that powers the simulation engine and general recommendations for using the software. It also provides a brief summary of the design of the application and gives a full reproduction of the R code that makes up the model. In this view, the application menu also gives a brief summary of user warnings.
Dosage comparisons
As a final consideration in our study, we directly compared four dosage scenarios in our simulation engine: 0.25 mg/kg q24h in the AM, 0.25 mg/kg q24h in the PM, 0.25 mg/kg q12h, and 0.5 mg/kg q12h. In our simulation application, we set the engine to compare the median AUEC of 500 dogs (matched between virtual trials), at a sampling rate of 500 times over a period of 25 virtual days. The median AUEC comparison was made on day 20 over a period of 24 h. The long virtual time of simulation assured the simulated dogs reached steady state PD of benazeprilat. For 0.25 mg/kg q24h, independent of the time of dosing, we saw an approximate 55% decrease compared to placebo for AngII and a 95% increase in Ang(1–7). With a schedule of 0.5 mg/kg q12h, we saw an approximate 80% decrease versus placebo for AngII and 135% increase in Ang(1–7). Overall, a greater daily biomarker variance was observed with q24h (vs. q12h) dosing. Summary results are tabulated in Table 2 while median time-courses are plotted in Fig. 8.
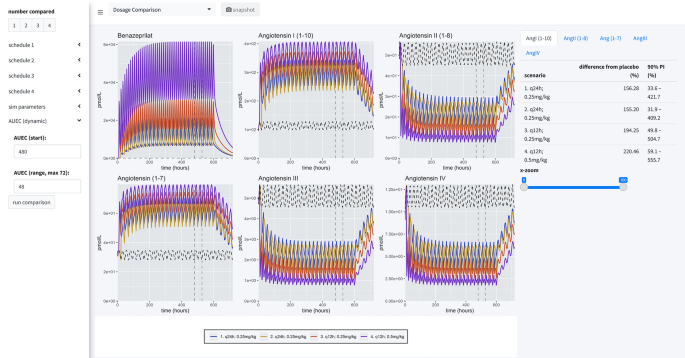
Simulation summary. Four administration schedules are compared in this simulation scenario: (1) 0.25 mg/kg every 24 h at 8 a.m.; (2) 0.25 mg/kg every 24 h at 8 p.m.; (3) 0.25 mg/kg twice a day at 8 a.m. and 8 p.m.; (4) 0.5 mg/kg twice a day at 8 a.m. and 8 p.m. 500 individuals were simulated for each scenario (for a total of 2500 individuals, with placebo). Curves are the me...
Comments
Post a Comment